Etude du sandow pour GPR

 Page créée le 19 mars 2004 et actualisée le 07 décembre 2005

ABAQUE

Pierre s'adresse d'abord aux passionnés de calculs - ici, appliqués aux grands planeurs lors de leur mise en l'air à l'aide d'une catapulte ! Après cette lecture - attentive - plus jamais vous ne resterez insensible au charme et à l'élégance d'un catapultage ...GR 

Le sandow et les grands planeurs

Le védépiste attiré par les grands modèles se trouve parfois confronté au problème du lancement de son planeur. -Il se retrouve seul et pour des raisons qui lui sont propres n’envisage pas de tenir le planeur à bout de bras, la radio suspendue à la dragonne ou comme je l’ai parfois vu, l’émetteur posé à même le sol.

-Il n’est pas seul mais les lanceurs potentiels ne l’inspirent pas (j’ai été il y a quelques années le piètre lanceur d’un 5 m au grand désespoir de son propriétaire et plus récemment le pilote victime de 2 lancers foireux consécutifs d’un mien 5 m / 10 kg).

-Son planeur est manifestement trop lourd et volumineux pour espérer un lancement manuel réussi.

-L’altitude ou les conditions météo ne permettent pas d’assurer un lancer sûr même de la part d’un lanceur chevronné.

Pour pallier les conséquences de ces situations, l’utilisation d’un sandow bien adapté au planeur à propulser est une solution envisageable.

Comme je n’avais pas de connaissances en la matière et que personne dans le microcosme védépiste du Menez-Hom ne pratique ce type de lancement, j’ai voulu éclairer ma lanterne et après avoir trouvé sur Internet une page de formules relatives à l’énergie de l’oscillateur harmonique, je me suis lancé dans la recherche de l’application de ces formules à notre loisir et plus précisément celui du lancer des grands planeurs à la pente. Le texte qui suit résume mes cogitations et vous fait part du résultat de mes expériences.

  Le créneau retenu

Il s’agit de lancer des planeurs d’une envergure supérieure à 4 m et d’une masse dépassant 5 kg.

Si, au moment du lâcher, la trajectoire du  planeur lancé à la main est légèrement descendante, quelquefois horizontale mais surtout pas ascendante, on considèrera dans ce qui suit que le sandow imprime au planeur une trajectoire horizontale.

Le vent ne sera pas pris en compte dans les calculs théoriques. S’il y en a, il améliorera la vitesse relative par rapport à l’air ambiant et apportera un bonus.

Petite remarque

Les grandes plumes ayant généralement un aspect maquette ou semi, le crochet extérieur ne sera pas de mise; il sera remplacé par un tube interne dans lequel viendra se loger une petite longueur de corde à piano solidaire du sandow. Cette solution m’avait été suggérée par un modéliste alsacien il y a bien une dizaine d’années mais je ne l’avais encore jamais mise en application.

 Autre solution : on conserve la même disposition angulaire mais la broche s'escamote (vers l'intérieur du fuselage) avec l'aide d'un ressort de compression dès que l'effort latéral a disparu. Cette broche possède une gorge demi ronde à 8 mm de son extrémité pour accueillir et immobiliser un anneau classique de catapulte. Pb : comment ressortir la broche ? plusieurs solutions ! GR

Lorsque le sandow se sera détendu, la

corde à piano quittera son logement

par son propre poids.

La corde à piano est reliée par

Explication : la tresse de 3 à 4 mètres est reliée à la broche sans la présence d'un anneau, le jeu est tel qu'il permet de libérer la broche dès que la tension a disparue.

Attention cette masse d'acier au bout d'un sandow est potentiellement dangereuse !  Le tube de 10 mm doit être collé très solidement sur la cellule ( résine époxy + fibre) sur une grande surface car cette zone du fuselage subit des chocs importants qui pourraient décoller le support du tube...GR

La théorie des élastiques

Pour une longueur donnée, on peut caractériser les élastiques par le poids qu’il convient de leur appliquer afin qu’ils s’allongent tous de la même valeur.

Considérons 3 élastiques E1, E2, E3 de natures différentes, de même longueur L0, suspendus au plafond. Si j’accroche à chacune de leur extrémité libre un poids de même valeur P, ces élastiques s’allongeront différemment de: a1 pour le premier, a2 pour le deuxième et a3 pour le troisième.

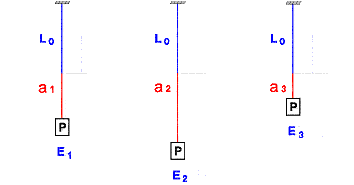
                           Fig. 1

Dans le langage courant, on dira que E3 est le plus raide et que E2 est le plus mou des trois puisque E3 s’est moins allongé que E1 et E1 moins que E2. Mais comme on va faire un peu de physique, on va quantifier cette raideur en attribuant à chaque élastique un coefficient qui permettra de prévoir leur comportement respectif sous différentes contraintes.

Imaginons que les allongements des élastiques soient:

              a1 = 0,80 m, a2 = 1,25 m, a 3 = 0,40 m, et que la charge P identique dans les 3 cas soit 10 kg.

On définit chacun des élastiques par la charge P qu’il convient de lui accrocher pour qu’il s’allonge de 1m. Cette charge baptisée K, est considérée constante dans le domaine de l’exploitation que nous ferons de l’élastique.

 Ceci revient à dire que l’allongement de l’élastique est proportionnel à la charge qui lui est appliquée et que l’on n’atteint pas le domaine de sa déformation plastique. Lorsque la charge aura disparue, il n’y aura pas d’allongement résiduel permanent.

Si E1 s’allonge de 0,80 m pour 10 kg, il faudra le soumettre à une charge de 10 / 0,80 = 12,50 kg pour qu’il s’allonge de 1 m. On dira que le coefficient K1 de E1 vaut 12,5 (sous-entendu 12,50 kg / m)

Pour E2, K2 vaudra 10 / 1,25 = 8 et pour E3, K3 vaudra 10 / 0,40 = 25

Ceci se traduit sous forme de formule par :

K = P / a

    (Coefficient = valeur de la charge divisée par valeur de l’allongement)

  De la longueur  de l’élastique

Admettons que la longueur L0 de nos 3 élastiques parfaits, non tendus soit 10 mètres. En raison de leur homogénéité on peut dire que chaque longueur unitaire – 1 cm par exemple – s’est allongée de la même quantité que celle de sa voisine soit :

pour E1 l’allongement unitaire est de 0,8 / 1000 = 0,0008 m  ou 0.08 cm.,

pour il est de E2 1.25 / 1000 = 0.00125 m ou 0,125 cm

et pour E3 il est de 0,4 / 1000 = 0.0004 m ou 0,04 cm.

Soient maintenant 3 élastiques E12, E22, E32, de 20 m au repos ayant respectivement les caractéristiques K de E1, E2 et E3.

Soumis à la charge de 10 kg comme tout à l’heure, chaque cm de ces élastiques s’allongera de 0,08, 0,125 ou 0,04 cm et les allongements correspondants seront

pour L12 de 0,08 x 2000 = 160 cm,

pour L22 de 0,125 x 2000 = 250 cm

et pour L32 de 0,04 x 2000 = 80 cm.

La longueur des élastiques étant doublée, les allongements sont doublés tandis que les coefficients K - rapports des charges aux allongements (K = P / a) - verront leur valeur divisée par 2.

Ce raisonnement simpliste mais vérifiable par l’expérience nous amène à dire que, toutes choses égales par ailleurs, plus la longueur est grande, plus K est petit ou encore que le coefficient K est inversement proportionnel à la longueur de l’élastique.

K = Ko . Lo / L

   De la section de l’élastique

Reprenons notre 2ème élastique du début, il a 10 m de long, et un K valant 8. Adjoignons en lui un 2ème identique en tous points. Si une charge de 10 kg est accrochée à leur extrémité libre commune, on admettra  que chaque brin supporte la moitié de la charge soit 5 kg et que l’allongement résultant pour chaque brin sera la moitié de ce qu’il est pour un brin soumis à 10 kg de charge. (Si K = P / a alors a = P / K)

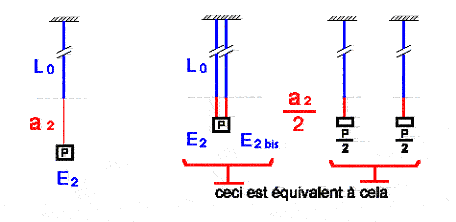
                            Fig. 2

Si donc l’allongement est divisé par 2 cela veut dire que le coefficient K résultant de l’assemblage des 2 brins sera multiplié par 2. Un raisonnement identique pour 2, 3, …n brins nous donnerait un K 2, 3 …n fois plus grand. On en conclut que K est directement proportionnel à la section de l’élastique.

Avec les conventions d’indice précédentes:

K = Ko x S / So

De la longueur et de la section de l’élastique

Reprenons encore une fois notre 2ème élastique du début, et replions le sur lui-même. Nous avons maintenant un élastique de 5 m de section doublée. Lorsque nous y accrochons une charge de 10 kg, nous pouvons considérer que chaque brin en supporte 5 et que finalement nous avons 2 élastiques de 5 m de long ayant un K de 16 (on vient de voir que K est inversement proportionnel à L) soumis chacun à une charge de 5 kg

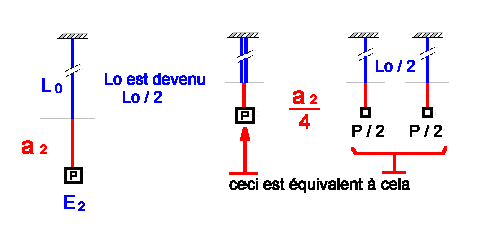
Fig. 3

L’allongement de chaque brin, en vertu de la formule K = P / a, sera a = P / K soit 5 / 16* = 0,3125 et le coefficient K résultant de la mise en parallèle des 2 brins: 10 / 0,325 = 32 c'est-à-dire 4 fois plus grand que celui de notre élastique d’origine (2 fois pour la longueur réduite de moitié et 2 fois pour la section qui a été doublée) de ceci résulte la petite formule  qui relie K, L et S :

K = K0.S / S0 x.L0  / L

* K pour un brin vaut 16 puisque la longueur d’un brin est Lo/ 2

Les énergies (petit rappel)

Lorsque une force F tend un élastique, le point d’application de cette force se déplace d’une longueur L,  elle effectue un travail quantifiable par

T = F . L

(Travail égal force multiplié par déplacement)

Une force résulte aussi du produit d’une masse par une accélération : F = m .g: (lire: f = m gamma).

Dans le domaine qui nous intéresse, nous pensons à l’accélération de la pesanteur. Elle prend comme valeur 9,81 m / s² dans le système d’unités que nous avons choisi.

Comme il convient d’être homogène dans les unités pour ne pas se mélanger les pinceaux, nous choisissons  comme unités de base:

•        Pour la longueur: le mètre m

•          Pour le temps la seconde s

•          Pour la masse le kilogramme kg

De ces unités de base il résulte que la force est exprimée en Newton N et le travail en Joule J

Prenons un exemple :

Une masse de 10 kg exerce sur sa surface d’appui une force F = m. g  de valeur : 10 x 9,81 = 98,1 N.

Si cette masse tombe d’une hauteur de 10 m elle effectue un travail T = F. L de 98,1 x 10 = 981 J

Dans le premiers paragraphes de cet article, j’ai volontairement occulté les Newton en utilisant le terme charge exprimé en kg  pour ne pas démarrer par une définition des unités, ce qui aurait peut-être rebuté certains lecteurs.

Energie emmagasinée par l’élastique

Reprenons une fois de plus notre élastique N° 2: il a une longueur L0 de 10 m et supporte une masse de 10 kg. Il est donc soumis à une force de 10 x 9,81 = 98,1 N et, pour rester dans un système homogène d’unités, son coefficient K devient 8 x 9,81 =  78,48 N / m.

La masse de 10 kg étant descendue de 1,25 m a effectué un travail T = F .L  de: 98,1 x 1,25 = 123 J

En diminuant la valeur de son énergie potentielle la masse en a transmis une partie à l’élastique, celui-ci étant prêt à la restituer dès qu’il retrouvera sa liberté de mouvement.

On démontre (voir la théorie des énergies) que l’énergie emmagasinée par l’élastique est la moitié de l’énergie potentielle que la masse aurait perdue si elle était tombée librement de la même hauteur; dans notre cas l’élastique a emmagasiné 123 / 2 = 61,5 J.

On sait aussi (de la même théorie) que l’énergie emmagasinée peut être exprimée par :

E = 1/2 . K . a²

 (K est le coefficient vu tout à l’heure et a l’allongement de l’élastique).

Comme énergie et travail sont en physique deux termes représentant la même notion, ils sont exprimés par les mêmes unités, le Joule dans le cas présent.       

Cette formule attribuera à l’élastique une énergie emmagasinée de: 1/2 x 78,48 x 1.25² = 61,5 J

Restitution de l’énergie

Ne parlons plus d’élastique mais de sandow et gardons en mémoire que K est le quotient de la force par l’allongement.

Soit donc un sandow fixe à une extrémité et relié à un planeur à l’autre.

Fig. 4

Le sandow étiré de a  emmagasine sous forme d’énergie potentielle, une énergie égale à 1/2 K . a²

Lorsque le planeur est lâché et que le crochet C arrive en O, le sandow ne tire plus, il a libéré toute son énergie. Le planeur alors animé d’une vitesse V est détenteur, sous forme d’énergie cinétique de toute l’énergie libérée par le sandow.

Rappelons pour ceux qui l’auraient oublié que l’énergie cinétique pour un mouvement rectiligne est calculable par la formule:

E = 1/2 m.V²

Formulons l’égalité des énergies potentielles et cinétiques: 1/2 K . a² = 1/2 m.V².

La belle affaire me direz vous d’avoir écrit cela!

Mais oui, c’est une belle affaire puisqu’elle va nous permettre de calculer la vitesse à laquelle le planeur se libèrera du  sandow et devra voler de ses propres ailes.

Après une petite transformation de cette égalité, nous découvrons que la vitesse est égale à l’allongement du sandow multiplié par la racine carrée du résultat de la division du coefficient k par la masse du planeur. Ouf! (Vous voyez ici toute l’importance du bon choix des unités).

En d’autre termes on écrira: V = a. (K/m)1/2 et en fonction de la vitesse désirée associée à la masse du planeur on pourra déterminer les valeurs de a ou de K par les formules:

a = V (m /K)1/2 et  K = m V² / a².

Un petit exemple pour revenir sur terre

Un planeur de 5.5m d’envergure a une masse de 11 kg,

Le sandow  de 5 m  au repos a un K valant 12. (Valeurs tout à fait arbitraires)

Si la vitesse souhaitée est 10 m/s au moment de lâcher, le sandow devra être étiré de:

10 x (11 / 12)1/2 = 9,57 m ; il est évident que dans la pratique on ne s’embarrassera pas de tant de décimales et l’allongement du sandow sera estimé à 10 m.

L’expérience montre que les valeurs ainsi calculées sont vraiment optimistes et qu’il convient de tenir compte des différentes pertes d’énergie provenant du frottement du sandow sur le sol, du roulement du planeur sur une surface plus ou moins plane et herbeuse, de l’imperfection du sandow…

Pour tenir compte de ces pertes, je diminue de 30%* environ la valeur du coefficient K déterminé comme précédemment.

Dans le cas présent,  le K pratique vaudra 8,4 si les calculs lui ont attribué la valeur 12 et sur le terrain, le sandow sera étiré de 10 x (11 / 8.4)1/2 = 11,44 » 12 m

Depuis la rédaction de ce texte, les différents essais que j’ai pratiqués me font dire que la valeur de 30% est une moyenne pour terrain relativement uni; au Menez-Hom cette valeur est optimiste et il convient d’abaisser K de 50% environ sur la pente nord.

Détermination de la vitesse d’envol

Il est clair que tous ces calculs n’ont de sens que si l’on connaît la vitesse à laquelle le planeur doit être lâché.

Il me semble opportun de choisir la vitesse donnant la finesse maximale puisque c’est celle qui permettra au planeur de s’écarter le mieux de la pente aussitôt le décollage.

Pour déterminer la finesse max et la vitesse correspondante, j’utilise l’excellent logiciel Visuaero de Patrick Medard. Ce faisant, j’ai noté que dans la majorité des cas la vitesse à la finesse max est comprise entre 10 et 12 m/s. Il n’y aura donc pas de crainte à commettre une erreur grossière en se cantonnant dans ce domaine de valeurs.   

L’abaque

Soyons réaliste, j’imagine bien que vous n’allez pas sortir votre calculette, ordinateur portable, table de log ou autres joyeusetés du genre avant de propulser un planeur à la pente. A l’effet de couvrir le maximum de cas, j’ai crée un abaque à 4 entrées: masse du planeur, vitesse désirée, coefficient du sandow et allongement de celui-ci.

Fig. 5

Mode d’emploi :

La masse du planeur m et la vitesse V souhaitée déterminent à gauche le point A. Ce point rappelé côté droit en B sur la droite K correspondant au sandow utilisé a pour abscisse l’allongement a qu’il convient de donner à ce sandow.

L’application à l’exemple précédent affiche un résultat d’environ 11 m. 

Addenda

Je pourrais considérer en avoir terminé après la présentation de l’abaque mais je voudrais aussi calculer le temps de roulage du planeur pour savoir si calculant un sandow, je ne crée pas une catapulte. Pour cela je vais m’attarder un peu sur l’évolution de la vitesse du planeur et sur son accélération entre le moment où il n’est plus retenu et celui où il n’est plus propulsé par le sandow.

La mise en vitesse du planeur

Nous avons vu que la vitesse transmise par le sandow est déterminée par l’égalité de 2 énergies: celle que possédait le sandow et celle acquise par le planeur : 1/2 K. a² = 1/2 m. V ²

De cette égalité nous extrayons V qui vaut a.(K/m)1/2. Remarquant que K et m sont constants, nous déduisons que la vitesse du planeur est proportionnelle à la distance qu’il a parcourue. Ramené au cas de notre planeur de 11kg,  nous calculons une vitesse est de 0,44 m/s après 0,50 m de roulage, puis 0,87 m/s, 1,75 m/s,  2,62 m/s,  5,24 m/s, 10,48 m/s après 1 m, 2 m, 3 m, 6 m et 12 m de course.

L’accélération pendant la prise de vitesse

Le planeur tracté avance parce qu’il est soumis à une force. Cette force vient de l’énergie accumulée dans le sandow. Le coefficient K de ce sandow et son allongement a, détermine  une force F=K. a (voir en début d’article). Comme F est aussi m.g, je puis écrire : m .g = K. a.

J’en arrive à l’accélération g que je peux calculer par g = a. K / m

Comme pour la vitesse, K/m est constant et j’en déduis que g est proportionnel à l’allongement du sandow. L’allongement diminue dans le temps puisque le planeur avance ; l’accélération qui est maximale au moment où le planeur commence à rouler décroît linéairement avec la distance parcourue pour s’annuler lorsque le sandow ne tire plus.

Dans l’exemple choisi, l’accélération vaut 12 x 8,4 / 11= 9.16 m/s² au départ et 6 x 8.4 / 11= 4,58 m/s² à mi course.

Le temps du roulage   Très bonne question.

Son développement théorique sort du cadre de ce qui à mon avis est publiable dans une revue de loisirs. Le CALCUL n’est pas ce que je souhaite développer, aussi, je vous en ferai grâce mais pour satisfaire votre curiosité je vous donnerai simplement une petite formule qui permettra de le calculer.

T = 1/2.p. (m/K)1/2

Voyons ce qu’elle attribue à notre 5.5 m de 11 kg.

T= 1/2 x 3,14 x (11 / 8,4)1/2 = 1,80 s. ce qui me parait raisonnable.

Si le temps ainsi déterminé est < 1s, il est vraisemblable que vous n’aurez pas le temps d’intervenir quoiqu’il arrive pendant le décollage.

Vous frôlerez  la cata "pulte" ou "strophe". (Suffixe au choix.).

Le planeur étant ce qu’il est, il conviendra dans ce cas, de modifier les caractéristiques du sandow soit en le rallongeant soit en choisissant un caoutchouc de coefficient plus faible.

Toujours pour éviter des calculs, j’ai établi un abaque donnant pour différentes valeurs de T et M, le K du sandow à utiliser. Cette valeur rapportée dans le premier abaque permet de prédéterminer l’allongement à prévoir.

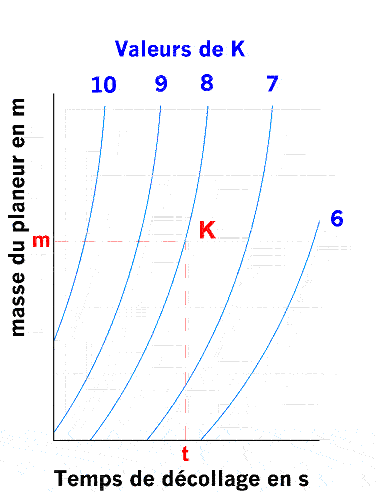
Fig. 6

Mise en Pratique

Afin de  mettre en pratique toute cette théorie, je prends dans mon parc de planeur un 4 m 7 kg.

Caractéristiques théoriques du sandow  - d’abord K puis L

- La valeur de K est déterminée à partir de la formule du temps de décollage

Comme T = 1/2 x p x (m / K)1/2, on calculera K par m x p² / (4 x T²)

Un décollage choisi en première approche à 1.5 s nécessiterait un sandow de

K = 7 x p² / (4 x 1.5²) = 7.68 N/m.

- La valeur de L sera calculée à partir de a =V x (m / K)1/2.

Avec k = 7.68, m = 7 et une vitesse de décollage de 10 m/s, il me faut un allongement de

a = 10 x (7 / 7,68)1/2 = 9,55 m.

Il restera à trouver un caoutchouc permettant un allongement de 10 m. Son K réel doit être:

Kr = 7.68 / 0.7 »11 N/m

Le sandow réel

Dans le commerce local j’ai acheté 10m de gomme carrée –celle qui sert à faire des lance-pierres- puis procédé à la détermination de son K.

1ère mesure

1 m de gomme s’allonge de 0,90 m environ pour une charge de  2.5 kg.

Pour ces valeurs, K = 2.5 x 9,81 / 0,9 = 22,07. Les 10 m de gomme ramèneront K à 2.2; si je n’en prends que 5 m, K vaudra 4,4. Comme le sandow doit s’étirer de 10 m, il faut une autre solution par exemple en doublant la gomme.

2ème mesure

Pour 1,07 m (je me suis trompé dans la mesure du mètre) de gomme en double, une masse de plomb de 2,5 kg provoque un allongement de 0,47 m.

J’en déduis Ko = 2,5 x 9.81 / 0,47 = 52,18.

La gomme en double, le sandow mesure 5 m et je peux l’étirer de 10 m

Son coefficient devient 52.18 x 1.07 / 5 = 11,17 soit 11,17 x 0.07 » 7,82 N/m.

J’avais déterminé coefficient de 7,68, Le K de mon sandow dépasse un peu cette valeur, voyons les nouvelles valeurs de l’allongement nécessaire et du temps de décollage.

L’allongement passe à 10 x (7 / 7,82)1/2 » 9,5 m (au lieu de 10) pour une vitesse d’envol de 10 m/s et un temps de décollage de T = p / 2 x (m / k)1/2 = p / 2 x (7 / 8.55)1/2 = 1.49 s (j’avais choisi 1,5 s)

La solution me parait bonne et mérite d’être essayée.

Les essais

Les essais ont eu lieu au Ménez-Hom le samedi 1er février de cette année.

1er essai. Le sandow de 10 m en monobrin est étiré de 10 m. Le planeur peine à démarrer, la corde à piano sort de son logement, le sandow se détend en oubliant le planeur.

Que le planeur peine à démarrer est tout à fait normal puisqu’il fallait 5 m de gomme en double - j’utilisais un sandow de K = 2,2 au lieu de 8,6 prévu - Mais que le planeur se décroche du sandow tendu l’est beaucoup moins. Le pourquoi a été trouvé en remarquant que la tête de la corde à piano solidaire du sandow frottait sur l’herbe et pouvait s’y accrocher en raison de la très faible vitesse du planeur. Il conviendra d’y remédier en sortant davantage la roue principale afin de surélever le planeur de quelques cm.

2ème essai.  Le sandow doublé mesure 5 m, son allongement est par prudence limité à 5 m. Au lâcher la prise de vitesse est plus franche mais insuffisante pour décoller.

C’est normal, il fallait tirer le sandow sur 9 m.

Le planeur ne s’est pas décroché, le sandow est resté légèrement tendu.

3ème essai.  Même sandow allongé cette fois de 11 m.

C’est tout bon! Le planeur prend une légère altitude avant de se décrocher; ceci est le résultat de l’excès de traction (11 m au lieu de 9 m).

Nème essai.  Des essais qui ont suivi on peut conclure provisoirement que:

1°/   9 m d’allongement suffisent pour décoller ce planeur sur une surface unie recouverte d’herbe rase.

2°/   J’ai correctement intégré les données de la théorie (et pan ! dans les chevilles).

3°/ Les frottements et causes diverses de la dégradation des résultats issus du calculs nécessitent le choix d’un K majoré de 25 à 50%. (Certains témoins de mes essais ont suggéré que le décollage se fasse roue rentrée si le planeur est équipé d’un train rentrant. )

4°/ La roue principale, si elle est fixe doit être suffisamment dégagée du fuselage afin de ne pas permettre le décrochage intempestif du planeur.

 5°/ Il parait indispensable de prévoir un dispositif de retenue de planeur afin que le pilote puisse aisément procéder seul à la mise en œuvre du sandow.    

Et pour conclure...

Ce qui précède ne concerne que le roulage pour prise de vitesse d’un planeur. Il n’a jamais été question de mise en altitude; cette action est menée à bien par la pompe de service après libération du sandow. La prise d’altitude à l’élastique (sandow ou catapulte) pourra faire l’objet d’un autre article si ma muse ne me trahit pas.

Bons décollages et bons vols à tous.